A High-Performance Hybrid Monte Carlo / Molecular Dynamics Framework For GROMACS

Introduction

Classical molecular simulation is becoming increasingly capable of investigating important questions involving self-assembly, molecular association, conformational heterogeneity and phase behavior in biophysics, engineering and material science. However, as hardware and software have improved, it has become increasingly challenging to combine novel methodological advances with the most advanced high-performance simulation engines. Ideally, this software needs to be available to a broad audience, and allow for simple maintenance. It also needs to be geared towards easy extensibility to facilitate further methodological advances.

Molecular dynamics (MD) and Monte Carlo (MC) are the main methods for sampling configurations in molecular simulations. Supporting both approaches allows for algorithms that accelerate sampling and increase functionality, such as MC barostats¹, nonequilibrium candidate MC², Gibbs ensemble MC³, enhanced alchemical sampling techniques^4,5,6, or configurational bias MC⁷.

This project is extending the popular GROMACS molecular simulation package⁸ to provide a high-performance framework to mix MC and MD methods. GROMACS owes its popularity among users (about 10,000 active users) and developers (42 unique code contributors over the last 3 years) to its open source nature and high performance⁹. The need for an extensible framework is easily seen by the number of forks of GROMACS which have implemented MC or hybrid MC/MD methods (see Refs^10,11,12 for a non-exhaustive list of such efforts), but have not been integrated into the main release of GROMACS to date.

Project timeline

2018 - 2019	Pre MolSSI funding: Previous work Modernization of the GROMACS simulator loop, aiming at <ul style='\"line-height:120%\"'>Modularizing components of simulation loopEncapsulating data in modules, defining remaining data dependenciesSimplifying maintenanceIncreasing extensibility</ul>
Jan - Jun 2020	First phase of MolSSI funded project: Foundation <ul style='\"line-height:120%\"'>Simplified creation of new algorithmsPrototype of the MC frameworkHybrid MC/MD proof of concept</ul>
Jul - Dec 2020	Second phase of MolSSI funded project: Implementation <ul style='\"line-height:120%\"'>Release GROMACS 2021Prototype of general collective variable description</ul>
Jan - Jun 2021	Third phase of MolSSI funded project: Application <ul style='\"line-height:120%\"'><li>Implement novel algorithms for GROMACS 2022 using MC/MD framework and CV description</li></ul>

2018 - 2019: Earlier work

Since 2018, I have been leading the effort to evolve the GROMACS MD simulator (the main simulation loop) from a largely procedural design, with poorly defined data dependencies between parts of the simulation loop, towards a modular, encapsulated design. The new modular simulator of GROMACS follows a number of design principles, including

• Definition of Elements: Elements are parts of the simulation loop carrying out a well-defined, limited functionality (e.g. force calculation, propagation of positions or velocities, accumulation of data over ranks, …). The entire simulation consists of elements being repeatedly called in a prescribed order. The order of the elements defines the simulation algorithm. See Listing 1 for an illustrative example of important interfaces and classes.
• Data encapsulation: Elements own their data. Elements only share data over well-defined interfaces.
• Client system: Infrastructure elements such as trajectory writing, checkpoint facility, data communication between simulation ranks, etc are agnostic of the simulation algorithm or implementation details of other elements. They merely offer a narrow functionality that can be used by registered elements, their clients. See Prototype of the Monte Carlo framework for an example of the client system.

This simplifies the maintenance and increases the extensibility by making the rearrangement of components straightforward. GROMACS 2020 ships with an initial version of the modular simulator with a reduced feature set.

class ISimulatorElement {
public:
    //! Called once at beginning of simulation
    virtual void setup() = 0;
    //! Called once at end of simulation
    virtual void teardown() = 0;
    //! Allows element to schedule task at specific time / step
    virtual void scheduleTask(Step, Time, const RegisterRunFunctionPtr&) = 0;
}

class SimulatorAlgorithm final {
public:
    /*! \brief Get next task in queue
     *
     * This function will repeatedly loop over elements list
     * until end of simulation, calling scheduleTask() to
     * query whether element needs to run. Task list can be
     * precomputed to increase performance. */
    [[nodiscard]] const SimulatorRunFunction* getTask();
private:
    //! The list of element defining the algorithm
    std::vector<ISimulatorElement*> elements;
}

// Implement general GROMACS simulator interface
class ModularSimulator final : public ISimulator {
public:
    //! Set up and run a simulation (only function of interface)
    void run() override {
        auto algorithm = createAlgorithm();
        while (const auto* task = algorithm.getTask()) {
            // execute task
            (*task)();
        }
    }
private:
    //! Create algorithm by emplacing elements in right order
    SimulatorAlgorithm createAlgorithm();
}

Listing 1: Simplified declarations of the most relevant modular simulator interfaces and classes.

January to June 2020: Foundation

Simplify the creation of new algorithms

While earlier efforts modularized the components of the GROMACS simulation loop, the definition the order of modules (which in turn defines the simulation algorithm) remained cumbersome. A new builder approach allows developers to see at one glance what components make up the algorithm.

Figure 1: Definition of an identical NVE leap frog algorithm in GROMACS 2020 vs GROMACS 2021-dev.

The earlier version was cumbersome because the user was required to connect elements explicitly during the creation of the algorithm. This required elements to be built in a very specific order, which strongly limited extensibility. The simplification is achieved by leveraging the strengths of the modular simulator design. As the interactions between elements are reduced to well-defined interfaces, they can be connected automatically, allowing the user to simply add element in the desired order, and let the algorithm builder take care of the connection details.

Prototype of the Monte Carlo framework

Following the design principles of the modular simulator, a prototype of the Monte Carlo framework was implemented. The design follows the client system: The Monte Carlo element allows other elements to register as clients. It informs its clients about when a state is saved, and when an earlier state needs to be restored. It also allows its clients to contribute additive terms to the energy expression used to determine whether a candidate state is accepted or rejected.

The MC element is not collecting the stored state, but requiring its clients to store their part of the state. This ensures that no unnecessary communication is required, and allows simulations including MC steps to retain a performance comparable to vanilla MD even in highly parallelized simulations.

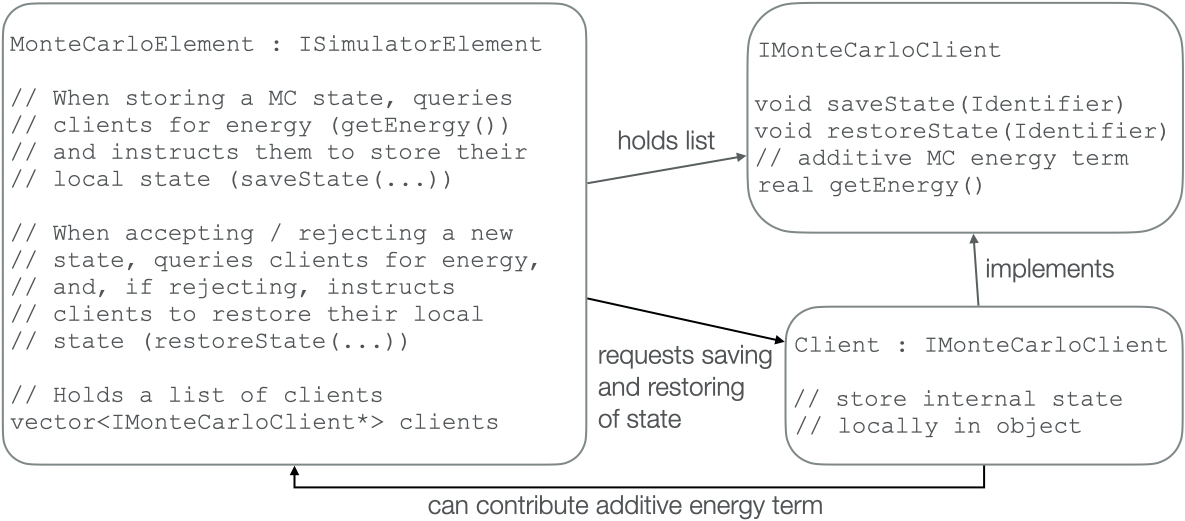
Figure 1: Illustration of the client system that allows to implement general MC algorithms. The MC element does not need to know implementation details of its clients, and the clients do not need to be aware of the details of the MC algorithm.

Hybrid MC/MD proof of concept

Combining the new algorithm creation syntax with the client-based MC prototype outlined above makes creating a hybrid MC/MD algorithm straightforward.

builder->add<MonteCarloElement>();
builder->add<ForceElement>();
builder->add<StatePropagatorData::Element>(); // full state at time t here!
builder->add<Propagator<IntegrationStep::LeapFrog>>(inputrec->delta_t);
if (constr)
{
    builder->add<ConstraintsElement<ConstraintVariable::Positions>>();
}
builder->add<ComputeGlobalsElement<ComputeGlobalsAlgorithm::LeapFrog>>();
builder->add<EnergyData::Element>(); // energies at time t here!

Listing 2: Definition of a hybrid MC/MD leap frog algorithm in GROMACS 2021-dev. The MC element added on the first line indicates where in the loop MC states are saved / restored.

The addition of the MonteCarloElement on the first line of the snippet turns the NVE algorithm shown above into a hybrid MC/MD simulation. Clearly, the above snippet hides some complexity. The StatePropagatorData::Element (holding the current microstate of the system) is registered to the MC element, such that it can back up a copy of its state for later restoring. The MC element uses an interface to query the EnergyData for current energies. The exact acceptance / rejection criterion used by the MC element is defined in the simulation input file. This complexity is, however, encapsulated in a way that it does not reduce extensibility or maintainability.

Future work

July to December 2020: Implementation

Release GROMACS 2021: We aim at delivering GROMACS 2021 (beta mid September, release end of the year) with

• a fully-featured modular simulator (all functionality available in the legacy implementation also available in the modular simulator),
• hybrid MC/MD capability, and
• an MC barostat that can replace other pressure control algorithms in standard MD simulations.

Prototype of a general collective variable description

A GROMACS-internal representation of collective variables (CVs) will greatly increase the flexibility of the hybrid MC/MD framework. The nonequilibrium candidate Monte Carlo formalism allows users to apply an external force to a system over a short period of time followed by a Metropolis acceptance step to recover equilibrium properties. The ability to apply this force to complex CVs opens up new possibilities for novel enhanced sampling¹³.

Simple examples of moves in CV space include forced rotations around dihedral angles, forces along the distance between atoms, and movement along harmonic modes of a system. These CVs can be much more complex, e.g. a combination of predefined functions of atom positions, such as generated by neural nets or combination of arbitrary basis functions.

Defining forces on CVs will require a module able to translate these CV forces into forces on single atoms, and provide the single-atom forces to the system. The general framework to implement such force providers is already available in GROMACS.

January to June 2021: Application

In view of GROMACS 2022, we will leverage the combination of the hybrid MC/MD framework and the general collective variable representation to implement novel algorithms.

Acknowledgements

Pascal T. Merz was supported by a fellowship from The Molecular Sciences Software Institute under NSF grant OAC-1547580. Pascal T. Merz wishes to thank Michael Shirts (University of Colorado Boulder), Eliseo Marin-Rimoldi (Molecular Sciences Software Institute), Paul Bauer and Mark Abraham (KTH Stockholm), M. Eric Irrgang (University of Virginia), and the entire GROMACS developer team for their support.

References

1. Johan Aqvist, Petra Wennerström, Martin Nervall, Sinisa Bjelic, and Bjørn O. Brandsdal. Molecular dynamics simulations of water and biomolecules with a Monte Carlo constant pressure algorithm. Chemical Physics Letters, 384(4):288–294, 2004. doi: 10.1016/j.cplett.2003.12.039. ↩

2. Jerome P. Nilmeier, Gavin E. Crooks, David D. L. Minh, and John D. Chodera. Nonequilibrium candidate Monte Carlo is an efficient tool for equilibrium simulation. PNAS, 108(45):E1009–E1018, 2011. doi: 10.1073/pnas.1106094108. ↩

3. Athanassios Z. Panagiotopoulos. Direct Determination of Fluid Phase Equilibria by Simulation in the Gibbs Ensemble: A Review. Molecular Simulation, 9(1):1–23, 1992. doi: 10.1080/08927029208048258. ↩

4. Jozef Hritz and Chris Oostenbrink. Hamiltonian replica exchange molecular dynamics using soft-core interactions. J. Chem. Phys., 128(14):144121, 2008. doi: 10.1063/1.2888998. ↩

5. Wei Jiang and Benoît Roux. Free Energy Perturbation Hamiltonian Replica-Exchange Molecular Dynamics (FEP/H-REMD) for Absolute Ligand Binding Free Energy Calculations. J. Chem. Theory Comput., 6(9):2559–2565, 2010. doi: 10.1021/ct1001768. ↩

6. Lingle Wang, Richard A. Friesner, and B. J. Berne. Replica Exchange with Solute Scaling: A More Efficient Version of Replica Exchange with Solute Tempering (REST2). J. Phys. Chem. B, 115(30): 9431–9438, 2011. doi: 10.1021/jp204407d. ↩

7. Jörn Ilja Siepmann and Daan Frenkel. Configurational bias Monte Carlo: A new sampling scheme for flexible chains. Molecular Physics, 75(1):59–70, 1992. doi: 10.1080/00268979200100061. ↩

8. Mark James Abraham, Teemu Murtola, Roland Schulz, Szilárd Páll, Jeremy C. Smith, Berk Hess, and Erik Lindahl. GROMACS: High performance molecular simulations through multi-level parallelism fromlaptops to supercomputers. SoftwareX, 1-2:19–25, 2015. doi: 10.1016/j.softx.2015.06.001. ↩

9. Carsten Kutzner, Szilárd Páll, Martin Fechner, Ansgar Esztermann, Bert L. de Groot, and Helmut Grubmüller. More bang for your buck: Improved use of GPU nodes for GROMACS 2018. Journal of Computational Chemistry, 40(27):2418–2431, 2019. doi: 10.1002/jcc.26011. ↩

10. Jason A. Wagoner and Vijay S. Pande. A smoothly decoupled particle interface: New methods forcoupling explicit and implicit solvent. J. Chem. Phys., 134(21):214103, 2011. doi: 10.1063/1.3595262. ↩

11. Mario Fernández-Pendás, Bruno Escribano, Tijana Radivojevic, and Elena Akhmatskaya. Constantpressure hybrid Monte Carlo simulations in GROMACS. J Mol Model, 20(12):2487, 2014. doi:10.1007/s00894-014-2487-y. ↩

12. Sebastian Wingbermühle and Lars V. Schäfer. On Obtaining Boltzmann-Distributed Configurational Ensembles from Expanded Ensemble Simulations with Fast State Mixing. J. Chem. Theory Comput., 15(5):2774–2779, 2019. doi: 10.1021/acs.jctc.9b00100. ↩

13. Donghyuk Suh, Brian K. Radak, Christophe Chipot, and Benoît Roux. Enhanced configurational sampling with hybrid non-equilibrium molecular dynamics–Monte Carlo propagator. J. Chem. Phys., 148(1):014101, 2018. doi: 10.1063/1.5004154. ↩