Relativistic Excited State Coupled-Cluster

Introduction

The goal of this project is to implement and improve the preformance of excited state coupled cluster singles and doubles (CCSD) calculations in the Chronus Quantum software package,¹ which can be used to generate absorption spectra in both the UV/Vis and X-ray range. This is acheived through two separate methods:

1. Equation of Motion CCSD (EOM-CCSD),^2,3 wherein a nonhermitian eigenvalue problem is solved to obtain excitation energies and their oscillator strengths

2. Time-Dependent EOM-CCSD (TD-EOM-CCSD)^4,5 wherein the dipole autocorrelation function is propagated forward in time, resulting in a time-domain spectrum which is then Fourier transformed into the frequency-domain in order to generate an absorption spectrum

These Coupled-Cluster calculations can include both scalar relativistic effects and spin-orbit coupling variationally by using the exact 2-component (X2C)⁶ wavefunction as our reference wavefunction for the coupled-cluster calculation. The inclusion of such relativistic effects is important when looking for fine structure in absorption spectra such as zero-field splitting and the splitting in the X-ray L- and M-edges.

Theory

The ground state CC wavefunction⁷ is comprised of an exponential operator acting on a reference wavefunction, \(\vert\Phi_0\rangle\):

\[\vert\Psi_{CC}\rangle = e^{\hat{T}}\vert\Phi_0\rangle\]

where \(\vert\Phi_0\rangle\) can either be the X2C ground state wavefunction or the generalized Hartree-Fock ground state wavefunction and the cluster operator, \(\hat{T}\), at the singles and doubles level is:

\[\hat{T} = \hat{T}_1 + \hat{T}_2 = \sum_{ia} t_i^a \hat{a}_a^\dagger \hat{a}_i +\frac{1}{4} \sum_{ijab} t_{ij}^{ab} \hat{a}_a^\dagger \hat{a}_b^\dagger \hat{a}_j \hat{a}_i\]

where solving for the \(t\)-amplitudes, \(t_i^a\) and \(t_{ij}^{ab}\), will allow the CC ground state energy to be obtained via:

\[E_{CC} = \langle\Phi_0\vert\hat{H}e^{\hat{T}}\vert\Phi_0\rangle\]

Equation of Motion

The excited state wavefunctions can be determined as eigenfunctions of the shifted similarity-transformed Hamiltonian:^2,3

\[\tilde{H} = \bar{H}-E_{CC}\]

Where the eigenproblem that we set out to solve is:

\[\tilde{H}\hat{R}_P\vert\Psi_{CC}\rangle = \omega_P\hat{R}_P\vert\Psi_{CC}\rangle\]

and

\[\langle\Psi_{CC}\vert\hat{L}_P\tilde{H} = \langle\Psi_{CC}\vert\hat{L}_P\omega_P\]

Where \(\vert\Psi_{CC}\rangle\) is the ground state CC equation and \(\omega_P\) is the excitation energy for state \(P\). The linear excitation and de-excitation operators, \(\hat{R}_P\) and \(\hat{L}_P\) respecitvely, can be used to calculate the oscillator strength for each excitation.

Real-Time Equation of Motion

Instead of solving this eigenproblem directly, we can instead propagate the dipole autocorrelation function forward in time.^4,5 The spectral lineshape function of the dipole autocorrelation function is:

\[I(\omega) = \sum_{\xi \in {x,y,z}} \int\limits_{-\infty}^\infty dt\,e^{-iwt} \langle M(0) \cdot M(t)\rangle\]

and more specifically, the coupled-cluster dipole moment function is defined as:

\[I(\omega) = \sum_{\xi \in {x,y,z}} \int\limits_{-\infty}^\infty dt\,e^{-iwt} \langle\Phi_0\vert(\hat{1}+\hat{\Lambda})\bar{\mu}_\xi e^{i\tilde{H}t}\bar{\mu}_\xi\vert\Phi_0\rangle\]

where \(\bar{\mu}_\xi\) is the similarity transformed dipole operator.

This propagation forms a time domain spectrum which can then be Fourier transformed using the Pade approximation to yeild a frequency domain absorption spectrum:

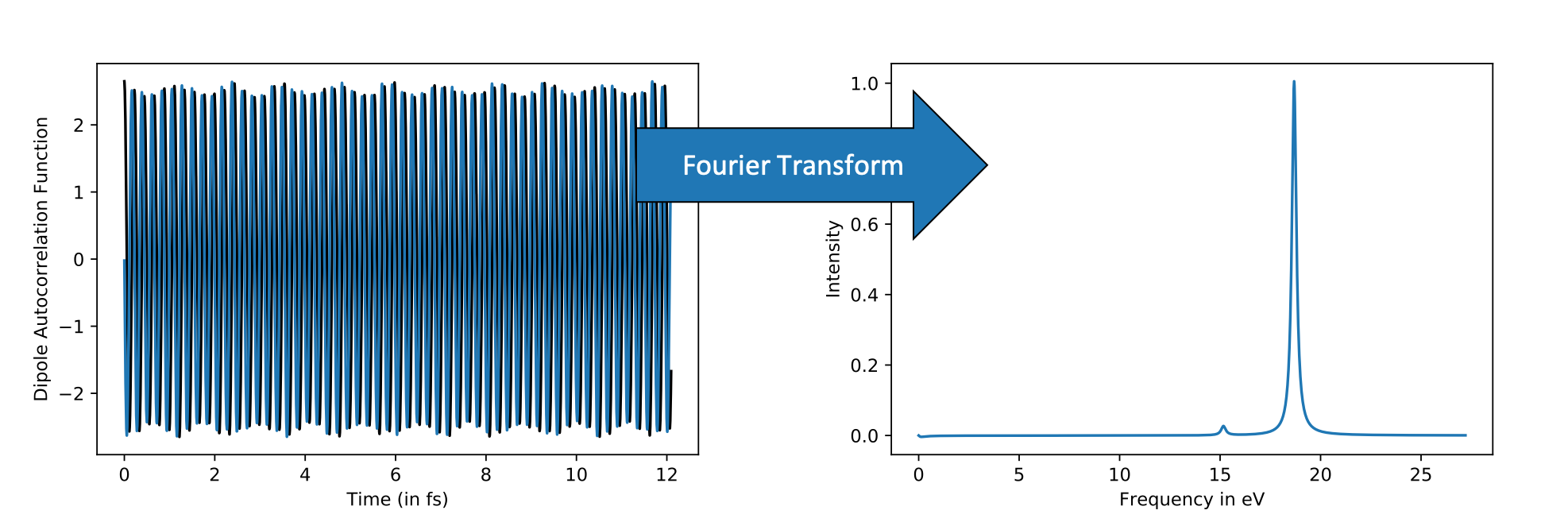
Figure 1: The time domain spectra on the left can be converted to the frequency domain absorption spectra on the right using a Fourier transformation. Data from STO-3G water molecule show.

Results

Zero-Field Splitting in Atomic Spectra

When ℂ-GHF is used as the reference wavefunction, only one transition is seen in this energy regime, from the \(^2S\) ground state to the \(^2P\) excited state. However, when using the X2C reference, the inclusion of relativistic effects, particularly spin-orbit coupling, allows the \(^2P\) states to split into \(^2P_{1/2}\) and \(^2P_{3/2}\) states. Additionally, the relative oscillator strength is as expected for the two- and four-fold degeneracy of the \(^2P_{1/2}\) and \(^2P_{3/2}\) states. It should also be noted that the excitation energies and oscillator strengths are in agreement in both the EOM-CCSD and TD-EOM formalisms.

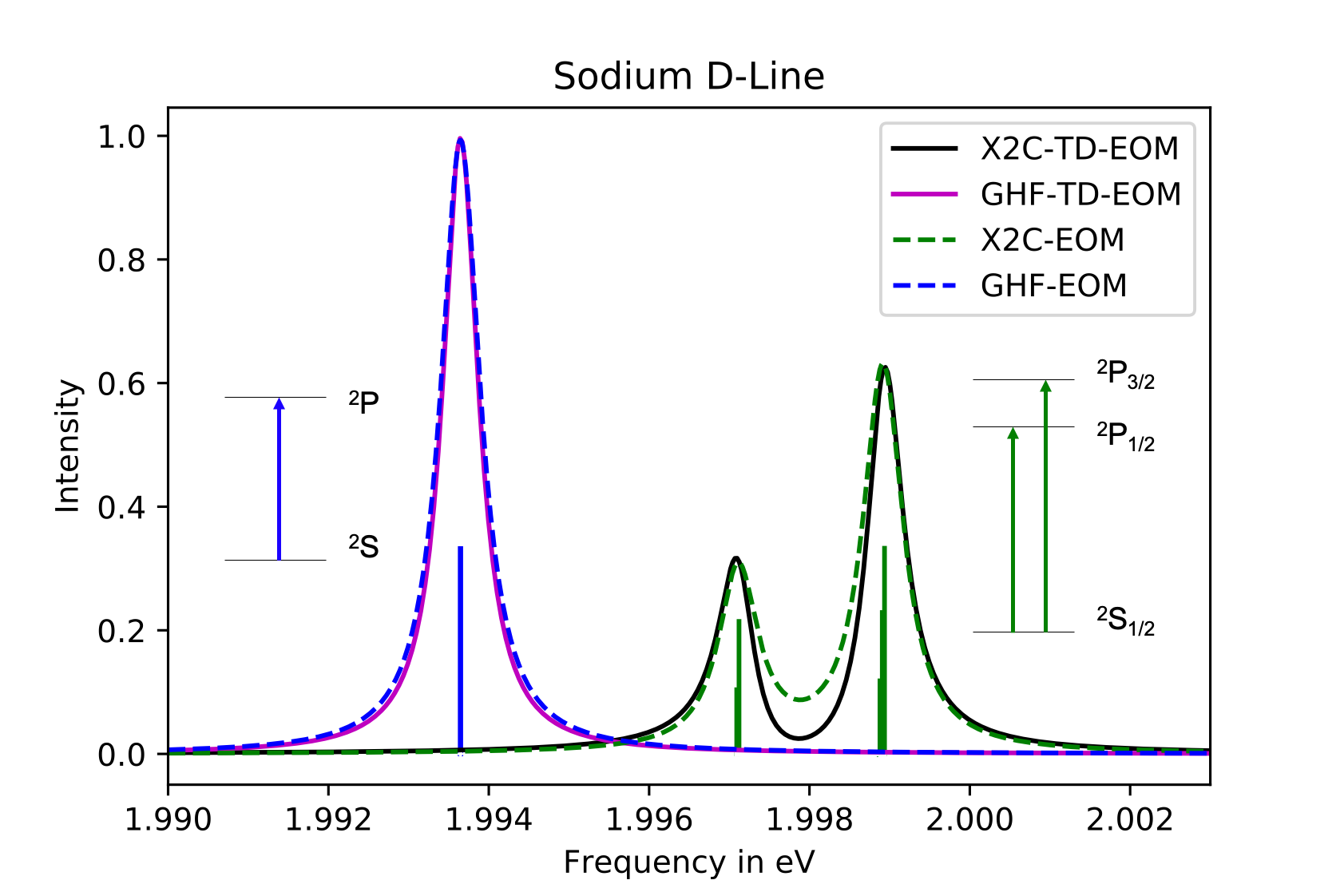
Figure 2: The low energy absorption spectra of a sodium atom using both nonrelativistic and relativistic caluclations for both the EOM and TD-EOM methods are shown, all using the 6-31G basis set.

A preliminary benchmark for the accuracy of TD-X2C-EOM-CCSD on Zero-Field splitting in atomic spectra can be found in Ref. 5.

L-edge X-Ray Spectra

Similarly, in the L-edge of Aluminum when the ℂ-GHF reference wavefunction is use we see transitions out of the 2p orbitals. However, when we use an X2C reference, the p orbitals split into \(J=\frac{1}{2}\) and \(J=\frac{3}{2}\), giving rise to the \(L_{2,3}\)-edge separation that can seen in Fig. 3. Again, there is good aggreement between the EOM-CCSD and TD-EOM formalisms.

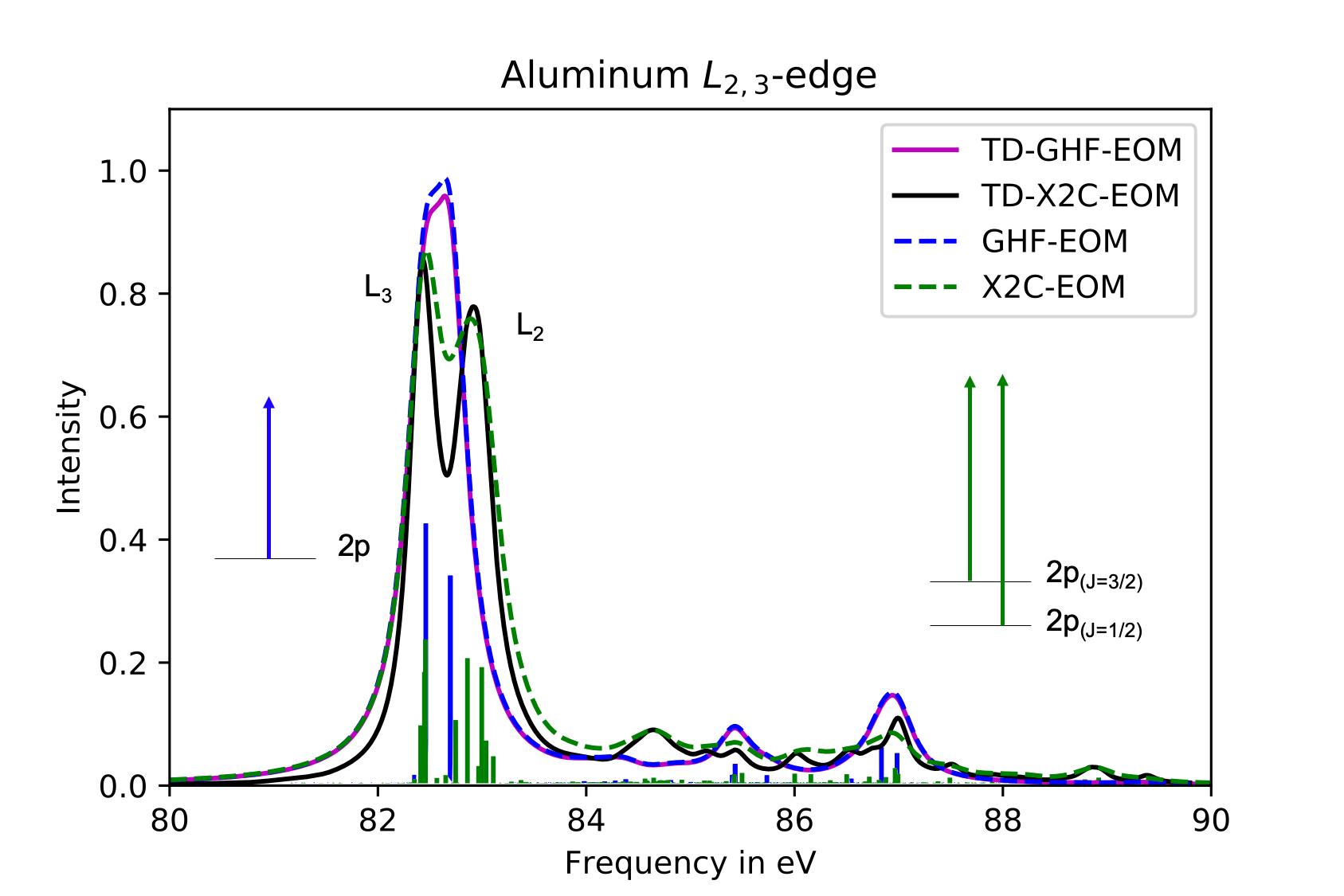
Figure 3: The X-ray absorption spectra of aluminum using both nonrelativistic and relativistic caluclations for both the EOM and TD-EOM methods are shown, all using the 6-31G basis set.

A benchmark for the accuracy of X2C-EOM-CCSD in both the US/Vis and X-ray region will be submitted by the end of the summer.⁸

Computational Analysis

Real-Time Propagators

Initially, fourth order runge-kutta (RK4) was used as the propagator for the implementation of TD-EOM. With the addition of the tensor contraction engine, Tiled Array,⁹ along with using the Lanczos method¹⁰ to propagate using a subspace Hamiltonian, has greatly improved the speed of propagation.
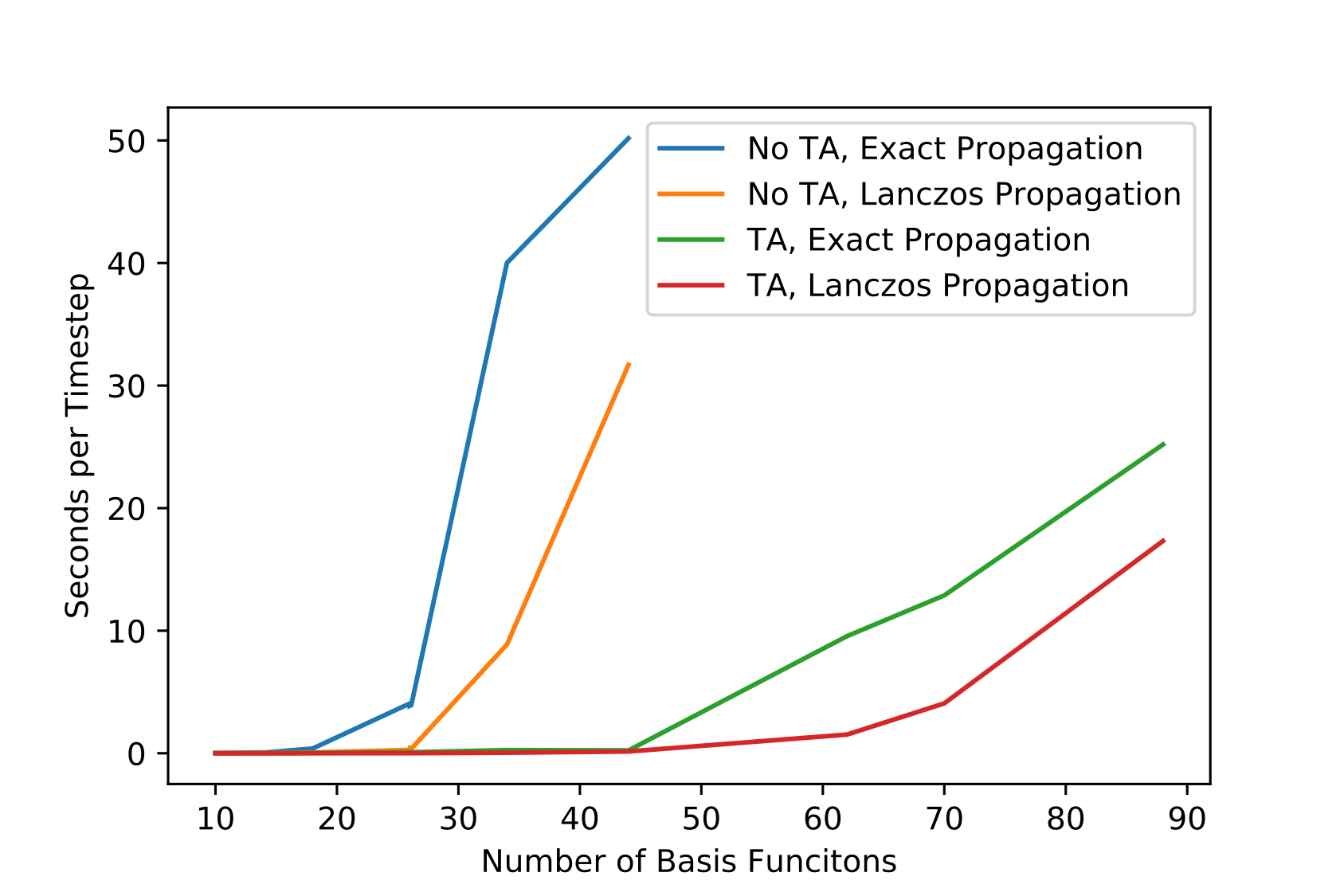
Figure 4: Timings of real-time propagation using Tiled Array (TA) and the Lanczos method.

When looking at systems with 26 basis functions, using Tiled Array alone provides an average speedup of over 40x, using Lanczos alone provides a speedup of over 10x, and when both Tiled Array and Lanczos are used an average speedup of over 350x is observed when compared to the initial RK4 implementation without the use of a tensor contraction engine.

References

1. D.B. Williams‐Young, A. Petrone, S. Sun, et al. The Chronus Quantum software package. WIREs Comput Mol Sci. 2020; 10:e1436. https://doi.org/10.1002/wcms.1436
2. J. F. Stanton, R. J. Bartlett. The Equation of Motion Coupled-Cluster Method. A Systematic Biorthogonal Approach to Molecular Excitation Energies, Transition Prob-abilities, and Excited State Properties.J. Chem. Phys.1993,98, 7029–7039. https://doi.org/10.1063/1.464746
3. I. Shavitt, R. J. Bartlett. Many-Body Methods in Chemistry and Physics; MBPT andCoupled-Cluster Theory; Cambridge University Press, 2009. https://doi.org/10.1063/1.464746
4. D. R. Nascimento, A. E. DePrince III. Linear Absorption Spectra from Explicitly Time-Dependent Equation-of-Motion Coupled-Cluster Theory. J. Chem. Theory Comput. 2016, 12, 5834−5840 https://doi.org/10.1021/acs.jctc.6b00796
5. L. N. Koulias, D. B. Williams-Young, D. R. Nascimento, A. E. DePrince III, and X. Li. Relativistic Real-Time Time-Dependent Equation-of-Motion Coupled-Cluster. J. Chem. Theory Comput. 2019, 15, 6617. https://doi.org/10.1021/acs.jctc.9b00729
6. W. Liu; D. Peng. Exact Two-component Hamiltonians Revisited. J. Chem. Phys. 2009, 131, 031104. https://doi.org/10.1063/1.3159445
7. D. T. Crawford, H. F. Schaefer III. Rev. Comp. Chem. 2007, 14, 33−136. https://doi.org/10.1002/9780470125915.ch2
8. L. N. Koulias, L. Lu, D. B. Williams-Young, T. Zhang, A. E. DePrince III, X. Li. Simulating Absorption Spectra with Relativistic Equation-of-Motion Coupled-Cluster Singles and Doubles. TBD.
9. “TiledArray: A general-purpose scalable block-sparse tensor framework”, Justus A. Calvin and Edward F. Valeev, https://github.com/valeevgroup/tiledarray
10. C. Lanczos. An Iteration Method for the Solution of the Eigenvalue Problem of Linear Differential and Integral Operators. Journal of Research of the National Bureau of Standards. 1950, 45 (4): 255–282. https://doi.org/10.6028/jres.045.026

Acknowledgements

“Lauren Koulias was supported by a fellowship from The Molecular Sciences Software Institute under NSF grant OAC-1547580”

Lauren would like to thank Professor Xiaosong Li and the entire Li research group for their support. Lauren would also like to thank her collaborators at Florida State University, particularly Brandon Cooper.