Pattern recognition based framework to characterize order in materials - Focus on block copolymer self assembly

Introduction

Block copolymers self-assemble to form a variety of different phases with highly regular patterns, depending on the microscopic ordering of molecules. Paramount to understanding and controlling this “order” is to have good “order parameters”, variables that can be used to track the changes occurring in the system as it transitions from disorder to order. Some common phases that block copolymers form include the lamellar, cylinder and gyroid network. This project uses molecular dynamics to simulate the growth of these phases from an isotropic liquid. We have developed local order parameters based on particle symmetries and geometrical constraints that can identify and track the nucleation and growth of ordered domains along the transition pathway [1]. The framework has been found to be extremely useful in understanding the self-assembly of other complex phases [2], and in estimating free energy barriers using rare-event sampling techniques (work ongoing).

Methods

For simplicity, the methods were developed on a nanoparticle model that has been shown to form the same phases as seen in block copolymers [3]. The aim was to capture key features of the local geometry of a phase by identifying symmetries that are unique to that phase. For the two-dimensional phases (lamellar and cylinder) this simply involved identifying the principal axis of symmetry (normal vector of the lamella plane or direction vector of the cylinder axis). The alternating gyroid network is characterized by I4132 symmetry, which can be identified using the Steinhardt bond order parameters [4] (a set of complex vectors). In essence, we assign a set of phase-signature vectors to each particle in the simulation. The dot product of neighboring vector pairs then tells us the extent of their correlation, a higher value indicating stronger correlation. We use this definition to differentiate between the “disordered” and “ordered” particles, after which a clustering algorithm is used to group all the ordered particles together.

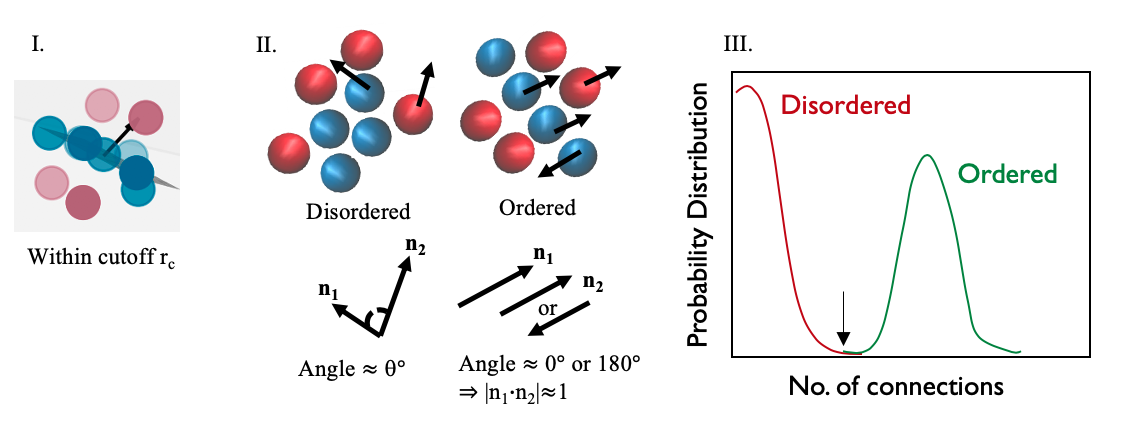
Figure 1: Depiction of steps to find Lamellar signature vectors and order parameter: I = Fitting a plane to same atom types and finding normal vector; II = Finding the angle between neighboring vectors; III = Comparing the distributions of the ordered and disordered phases.

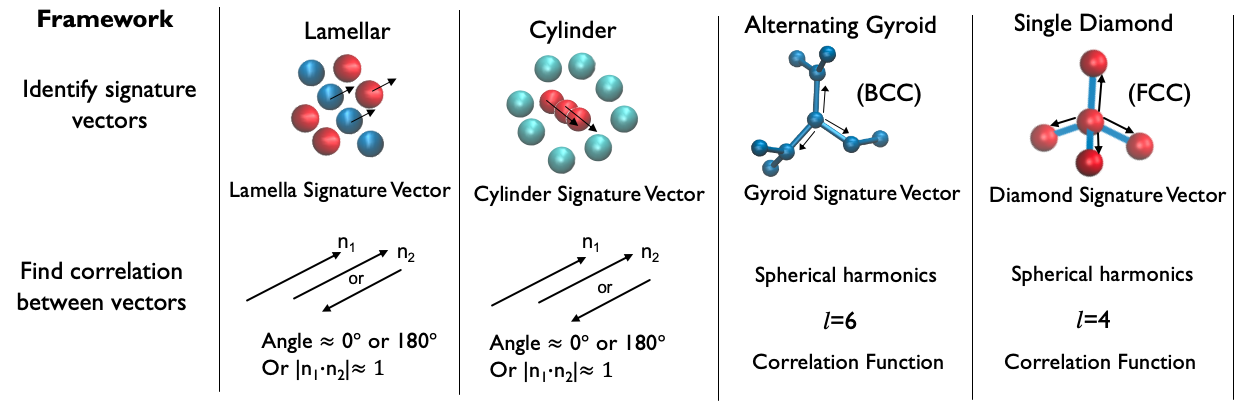Figure 2: Summary of the order parameter framework and the main steps involved.

Results

The order parameter framework was successful at tracking the phase behavior as it transitions from disorder to order. Figure below shows a visual representation of the lamellar phase vectors on a unit sphere (bottom row) that fully align at the poles as the particles arrange themselves into layers (top row). Thus, tracking the positions of the vectors gives us information about where we are in the phase transition.

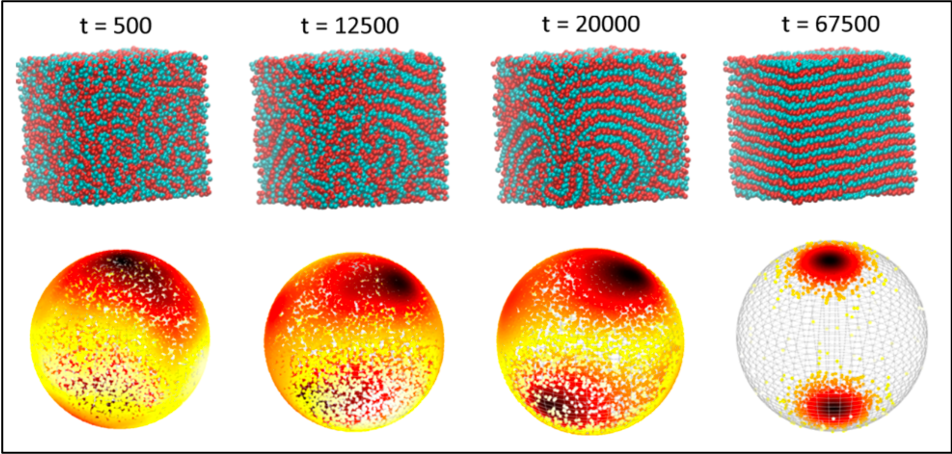Figure 3: Tracking the growth of the lamellar phase through the alignment of the signature vectors at different times (as seen in the spherical distribution plots).

Recent Efforts

More recent efforts have focused on using this framework – coupled with various sampling methods – to map the actual nucleation pathway of a system going from disorder to order. In particular, we have been focused on finding the free energy barriers for complex block copolymer phases, like the gyroid phase that we saw earlier, for which the transition mechanism is still not well understood. Work on this part is still ongoing, and has been the main focus of the MolSSI fellowship.

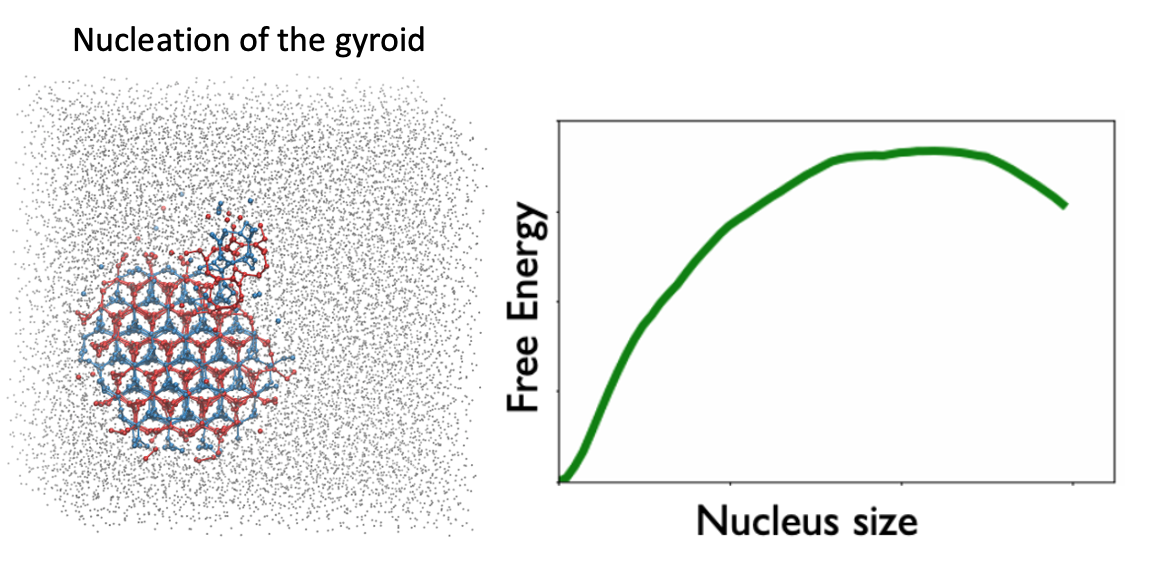Figure 4:Recent efforts have been aimed at mapping transition pathways for complex phases using the order parameters as reaction coordinates.

References

1. Mukhtyar, A. & Escobedo, F., Macromolecules 2018, 51, 23, 9769-9780
2. Mukhtyar, A. & Escobedo, F., Macromolecules 2018, 51, 23, 9781-9788
3. Kumar A., & Molinero, V., J. Phys. Chem. Lett. 2017, 8, 20, 5053–5058
4. Steinhardt, P. J., Nelson, D. R. & Ronchetti, M. Phys. Rev. B: Condens. Matter Mater. Phys. 1983, 28, 784

Acknowledgements

I would like to thank Eliseo Marin-Rimoldi and Matthew Welborn for their help and guidance on aspects of this project.

“Ankita J. Mukhtyar was supported by a fellowship from The Molecular Sciences Software Institute under NSF grant OAC-1547580”