Efficient implementation of ADC for ionization and electron attachment in molecules

Introduction

• Accurate computations of ionization potential (IP) and electron attachment (EA) are important for predicting properties of molecules and materials, such as redox potentials, band gaps, and photoelectron spectra.
• Development of reliable and efficient theoretical methods for computing IP and EA of molecules and materials is one of the current challenges in modern quantum chemistry.
• To address this problem, we developed a new and efficient computer implementation of algebraic diagrammatic construction theory (ADC) for simulating IP/EA of molecules in the open-source quantum chemical software package PySCF.

Theory

• Spectroscopic studies probe a molecular system by subjecting it to an external perturbation such as electromagnetic field and then studying the response of the system to that perturbation.
• The mathematical function required for computing the response is called a propagator.
• The IP/EA-ADC approximations are derived from a perturbative expansion of the one-electron propagator, poles and residues of which provide information about ionization and electron-attachment energies and transition intensities.

Implementation

• The present ADC implementation in PySCF can be applied to both closed- and open-shell molecules starting with either restricted or unrestricted Hartree-Fock orbitals.
• The key step of my IP/EA-ADC implementation is a function that defines the form of the \(\boldsymbol{\sigma} = \textbf{MX}\) vector that is the product of the ADC effective Hamiltonian matrix (\(\textbf{M}\)) and a trial vector (\(\textbf{X}\)).
• Once the \(\boldsymbol{\sigma}\) vector is defined for a particular ADC approximation, conventional iterative diagonalization techniques are used to solve for several lowest IP or EA energies and the intensities of these transitions.

^{Figure 1: A schematic representation of the IP/EA-ADC implementation in PySCF.}

Efficiency improvements to the previous IP/EA-ADC implementation

The pilot implementation of IP/EA-ADC was limited to systems with upto \(\sim\) 300 orbitals. As a part of my project supported by MolSSI, I made several improvements to increase the efficiency of my implementation in PySCF :

• Development of a spin-restricted ADC (RADC) code for closed-shell molecules

• An in-core algorithm with optimized memory and CPU efficiency

• An out-of-core algorithm that reduces the memory requirements by storing two-electron integrals on disk (using \(\textit{ h5py}\) Python module capabilities) and computing them on-the-fly. This is done using a buffering algorithm that computes subsets of the two-electron integrals which fits in the available memory.

• Use of Basic Linear Algebra Subroutines (BLAS) operations for expensive tensor contractions, which speeds up the calculations of the matrix-vector products (\(\boldsymbol{\sigma}\) = \(\textbf{MX}\))

• A modified ADC code interface to allow for a direct calculation of excitation energies and properties

• A modified preconditioner for Davidson’s iterative algorithm for better convergence of IP/EA energies

Results

• The several improvements discussed above have led to significant computational savings both with respect to memory usage as well as computational wall times.

• The new ADC implementation is more efficient than the highly optimized equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) implementation in PySCF and has a similar accuracy.

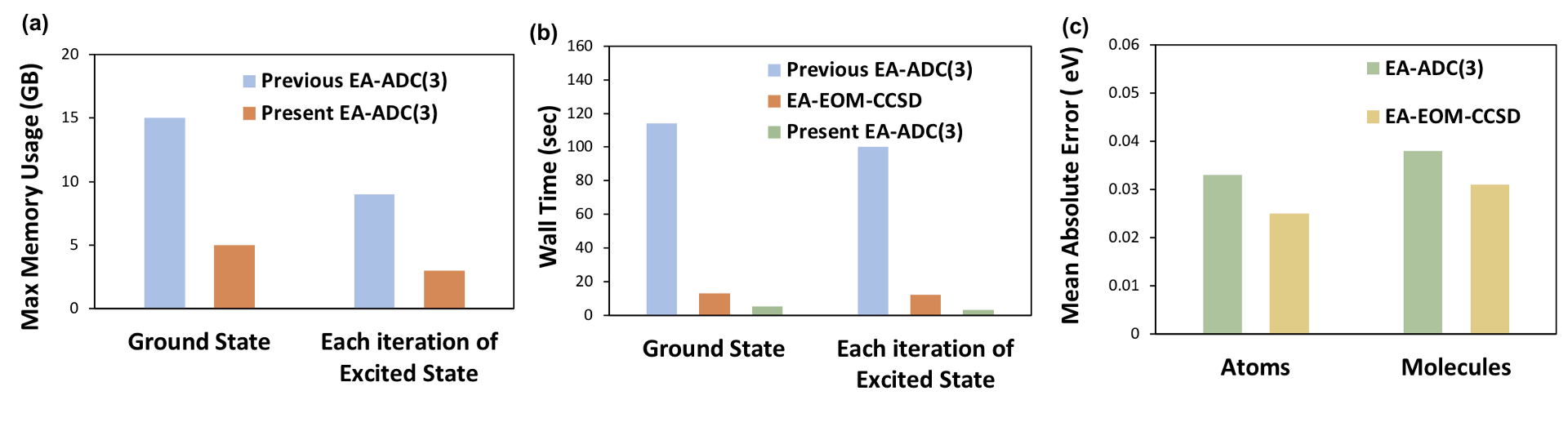^{Figure 2: Comparison of (a) maximum memory usage between the previous and present EA-ADC(3) implementations for H₂CO (basis set: aug-cc-pVTZ), (b) computational wall times between the previous and present EA-ADC(3) as well as EA-EOM-CCSD implementations for H₂CO (basis set : aug-cc-pVTZ), (c) mean absolute errors (eV) in EA’s for a set of closed-shell atoms and molecules simulated using EA-EOM-CCSD and EA-ADC(3) (basis set : aug-cc-pVQZ)}

• The present ADC implementation allows simulation of larger systems (600 orbitals) compared to the previous implementation which was limited to 300 orbitals.

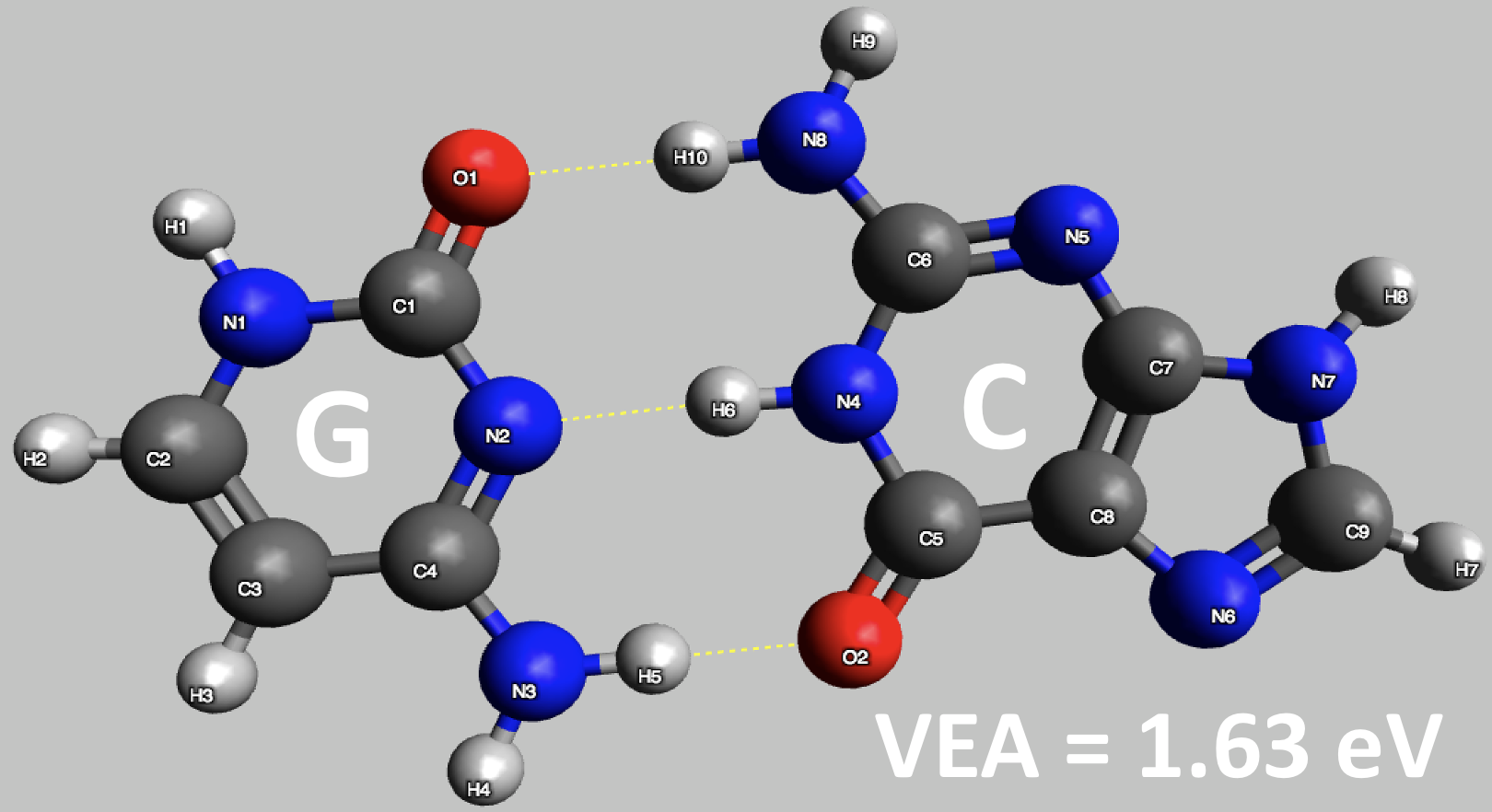
^{Figure 3: Preliminary results for vertical electron attachment energy of DNA nucleobase pair of guanine (G) and cytosine (C) computed using ADC(2) (basis set : aug-cc-pVDZ)}

Conclusion

• Implemented ADC as a new module in PySCF for accurate IP/EA simulation of molecules.

• Made several efficiency modifications leading to significant reduction in memory requirements and computational wall times.

• All the improvements enabled simulations of large molecules (600 orbitals), which paves the way for materials simulation using ADC in the future.

References

1. Schirmer, J. “Beyond the random-phase approximation: A new approximation scheme for the polarization propagator”, Phys. Rev. A,1982, 26, 2395

2. S. Banerjee, A. Yu. Sokolov. “Third-order algebraic diagrammatic construction theory for electron attachment and ionization energies: Conventional and Green’s function implementation”, J. Chem. Phys., 2019, 151, 224112

3. Q. Sun, et al. “Recent developments in the PySCF program package”,2020, In Review

Acknowledgements

“Samragni Banerjee was supported by a fellowship from The Molecular Sciences Software Institute under NSF grant OAC-1547580”