NeuralXC
A framework to train and deploy machine-learned density functionals
Introduction
- Solving the many-body problem in quantum mechanics requires the use of approximate methods
- These methods come in several flavors that differ in accuracy and computational cost (one usually increases with the other).
- For small molecules, highly accurate, explicitly correlated methods such as coupled cluster are usually feasible
- For larger systems (or longer timescales), these become too expensive and one has to revert to using faster low- level approximations.
- Our idea: Increase the accuracy of these approximations by adding a machine learned density functional (without losing performance, sacrificing some transferability)
Theory
Kohn-Sham Density Functional Theory
In KS-DFT, the many-body Schroedinger equation describing a complex quantum system is replaced by a simpler one-body equation describing a fictitious system of non-interacting particles. The energy of a system with electron-density \(\rho\) is then given as
\[E[\rho] = T_{s}[\rho] + \int_\mathbf{r} v_{ext}(\mathbf{r})\rho(\mathbf{r}) + E_{H}[\rho] + E_{xc}[\rho]\]In practice, the exact form of the exchange-correlation (xc) energy \(E_{xc} [\rho]\) is not known and several approximations that differ in accuracy and computational cost are being used.
NeuralXC
We show that a ML model can be trained to predict this xc-energy and subsequently used in self-consistent DFT calculations. The model input (features) is created by projecting the electron-density in real-space onto a set of atom-centered orthonormal basis functions \(\psi_{nlm}(\mathbf{r})\):
\[c^I_{nlm} = \int_\mathbf{r} \rho(\mathbf{r} - \mathbf{R}_{I}) \psi_{nlm}(\mathbf{r})\]A rotationally invariant version of these descriptors is then used by the model to predict atom-wise contributions to the xc-energy.
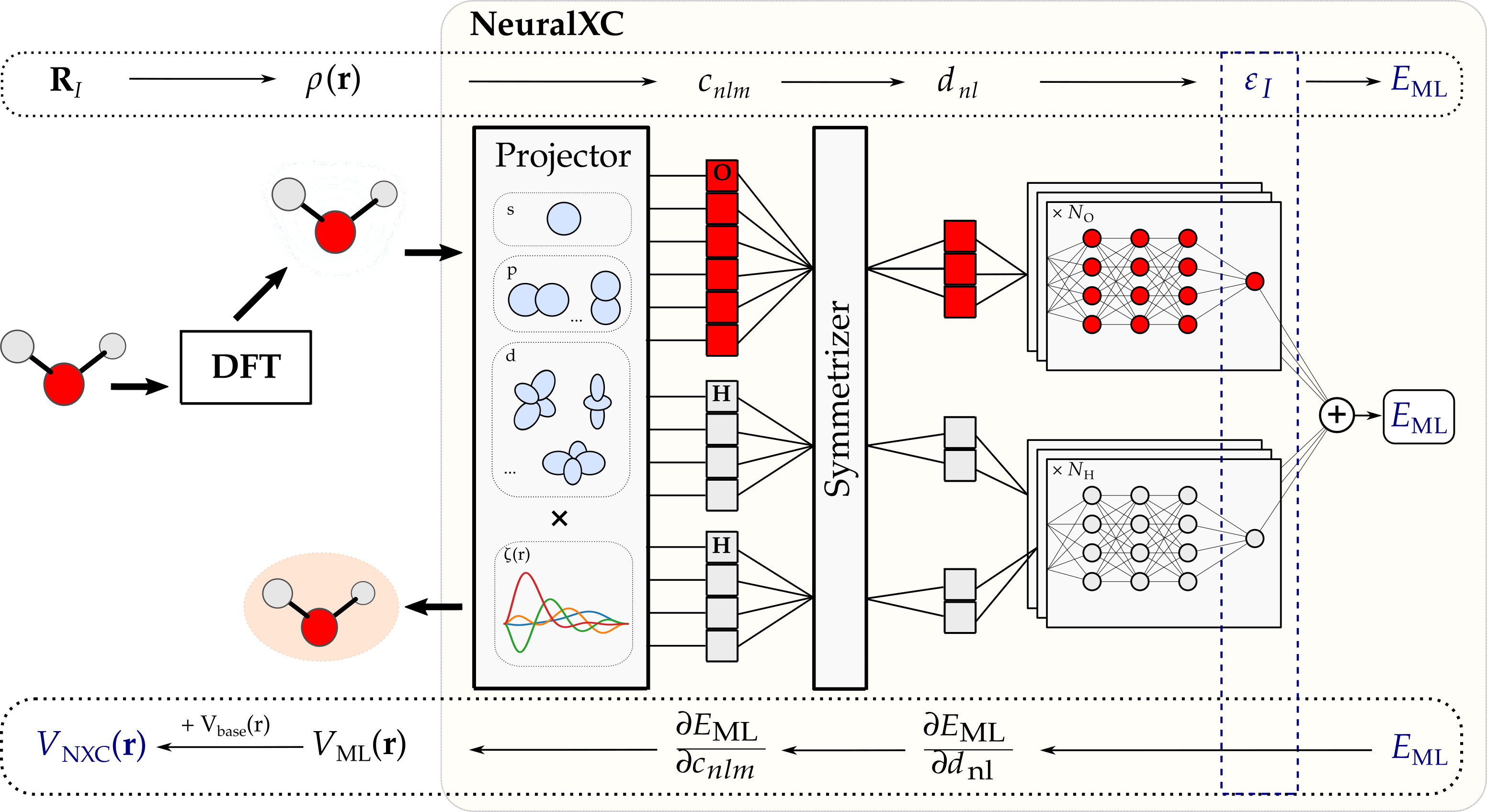
Figure 1: NeuralXC Architecture: Behler-type
neural network used to
fit the xc-energy. The
energy is implicitly
decomposed into atomic
contributions ensuring
permutation symmetry. The potential \(V_{NXC}(\mathbf{r}) = \delta E_{NXC}/\delta \rho(\mathbf{r})\) is obtained by back-propagating through the entire graph.
(from [1])
Results
Transferability
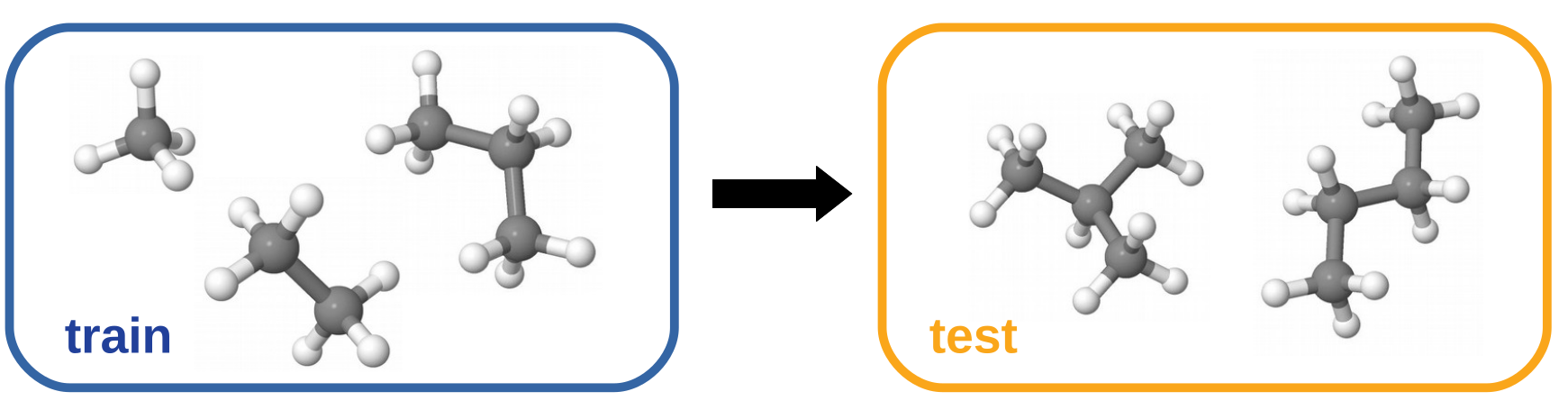
We trained a NeuralXC model on reference calculations of methane, ethane and propane obtained with coupled cluster with singles doubles and pertubative triples (CCSD(T)) using the cc-pVTZ basis set (data source: [2]). The model was subsequently tested on a hold-out set consisting of 100 samples of n-butane and isobutane. Excellent transferability to these systems with mean average errors (MAE) of about 6.5 meV can be observed.
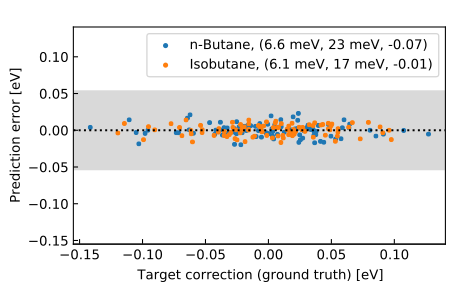
Figure 2: Residuals for transferability task on small alkanes, performance statistics are reported in the legend as (MAE, Max. absolute error, \(R^2\) of the residual error), errors were shifted to zero mean. (from [1])
Condensed systems and molecular dynamics
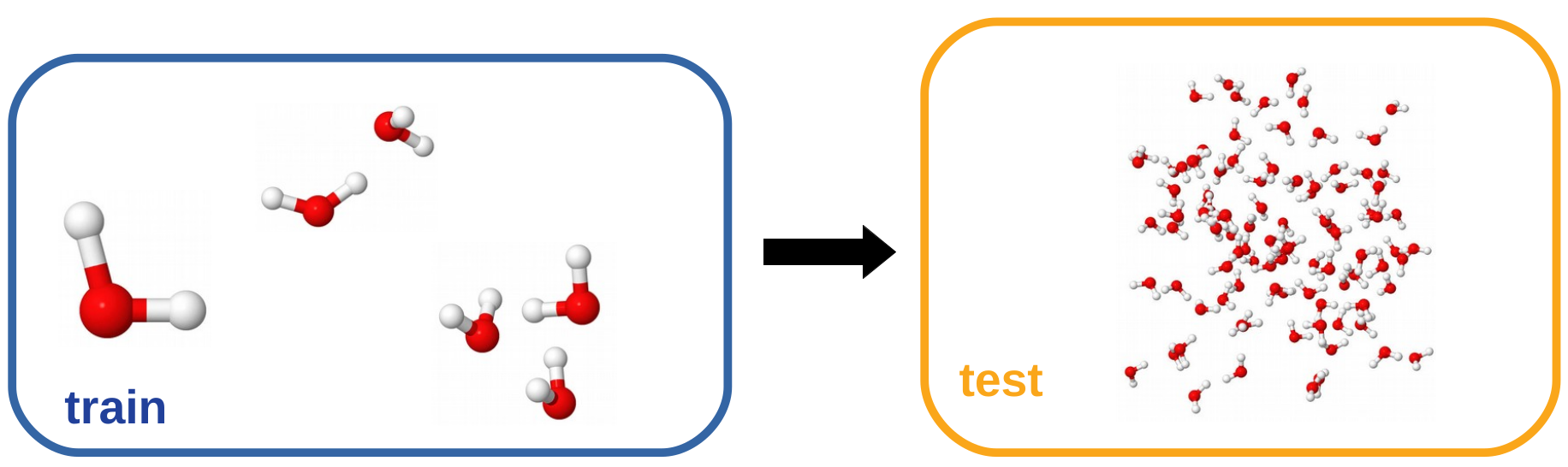
Moving on, we wanted to assess how the model generalizes to larger systems. To test this we trained a functional (from here on referred to as NXC-W01) on highly accurate (CCSD(T), CBS) calculations of 400 water monomers, 500 dimers and 250 trimers, provided by the authors of the MB-Pol water force-field [3, 4, 5]. The machine learned functional was built as an additive correction to PBE.
We used the fitted model to run a Born-Oppenheimer molecular dynamics simulation liquid water. The system was made up of 96 water molecules in a periodic box kept at experimental density and the average temperature was held at 300 K using stochastic velocity rescaling. The total simulation time was 20 ps of which the first 5 ps were used to thermalize the system and subsequently discarded.
As we currently cannot account for quantum effects we do not expect perfect agreement with experimental results. We can, however, compare our radial distribution fuctions (RDFs) to those obtained with MB-Pol, a force field that has been shown to provide an excellent treatment of water. The oxygen-oxygen RDF shows good agreement with MB-Pol results. Further, NXC-W01 outperforms state of the art density functionals such as SCAN and \(\omega\)B97M-V, all while being computationally more efficient.
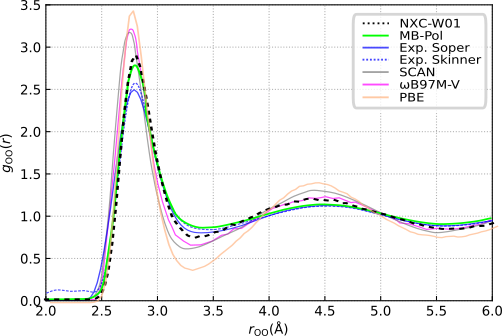
Figure 3: Oxygen-oxygen radial distribution function obtained from a molecular dynamics simulation of 96 water molecules in a periodic box. Experimental results by Skinner et al. [6] and Soper [7]. Scan results are taken from Ref. 8. \(\omega\)B97M-V results are from Ref. 9. (from [1])
We have also validated that NXC-W01 is capable of accurately describing bond breaking situations in water. Fig 6 shows the coordinated proton transfer reaction in a water-hexamer ring. None of our training data involved dissociated configurations, however NXC-W01 outperforms all other XC functionals and closely reproduces CCSD(T) results. These type of dissociative configurations are explored by ring polymer beads in path integral molecular dynamics simulations of liquid water[38], and cannot be accounted for with nondissociative force fields.
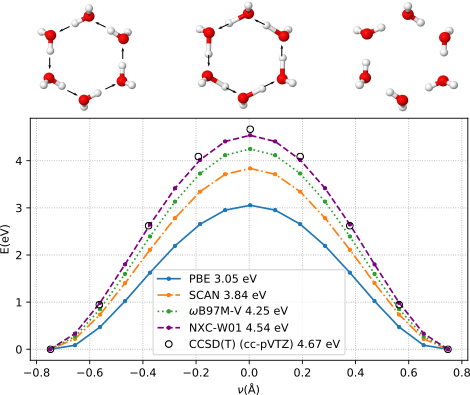
Figure 4: Proton transfer in a water hexamer ring. Potential energy compared to relaxed geometry as a function of the reaction coordinate \(\nu\). Energy barriers obtained with different approximations are given in legend. (from [1])
Implementation
The implementation of NeuralXC consists of two parts: a python framework to train and test functionals and a C++ library, libnxc, to deploy functionals.
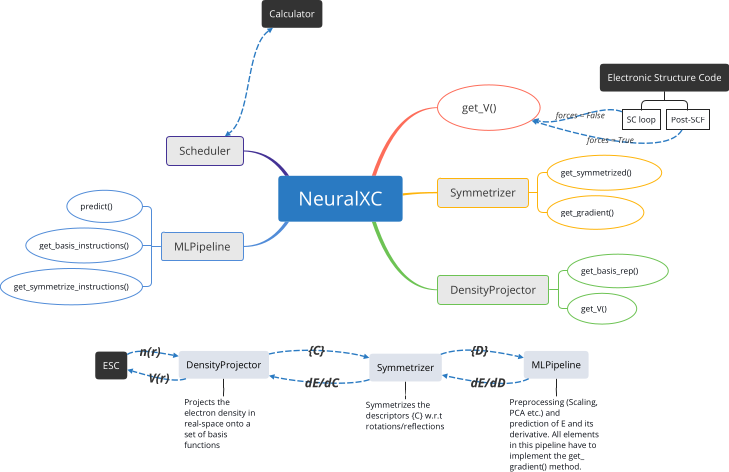
Figure 5: Python framework “NeuralXC”. Modular structure is imposed such that the user can easily customize basis-functions, machine learning pipelines etc.
Once the model is trained and tested it can be compiled into a Torch Script model which can subsequently be loaded by libnxc and used from within electronic structure codes. Currently supported codes include SIESTA and PySCF, but an expansion to other codes is planned for the near future.
Libnxc is inspired by libxc and is meant as a portable library of machine-learned functionals to be used in codes that already support libxc. It should be noted that libnxc is completely agnostic to the inner workings of the (compiled) machine learning model. Therefore the use of libnxc is not restricted to atom centered models as presented in this work but grid-based approaches such as the one proposed by Nagai et al. [ref] will also be supported.
Summary
- NeuralXC provides a way to create machine learned density functionals that lift lower level density functional approximations to the accuracy of a higher level method.
- Once trained, the functional can be used at small additional computational cost, scaling linearly with system size.
- Through its minimal interface, libnxc will enable the use of machine learned functionals in a wide variety of quantum chemistry and solid-state physics software.
Resources
References
1. S. Dick and M. Fernandez-Serra, Machine Learning Accurate Exchange and Correlation Functionals of the Electronic Density, Nat. commun. (accepted) (2020), doi:10.26434/chemrxiv.9947312.v3
2. Cheng, L., Welborn, M., Christensen, A. S. & Miller, T. F. Thermalized (350k) qm7b, gdb-13, water, and short alkane quantum chemistry dataset including mob-ml features (2019). URL https://data.caltech.edu/records/1177
3. Babin, V., Leforestier, C. & Paesani, F. Development of a first principles water potentia with flexible monomers: Dimer potential energy surface, VRT spectrum, and second virial coefficient. J. Chem. Theory Comput. 9, 5395403 (2013)
4. Babin, V., Medders, G. R. & Paesani, F. Development of a first principles water potential with flexible monomers. ii: Trimer potential energy surface, third virial coefficient, and small clusters. J. Chem. Theory Comput. 10, 1599607 (2014)
5. Medders, G. R., Babin, V. & Paesani, F. Development of a first-principles water potential with flexible monomers. iii. liquid phase properties. J. Chem. Theory Comput. 10, 29062910 (2014)
6. Skinner, L. B. et al. Benchmark oxygen-oxygen pair- distribution function of ambient water from x-ray diffrac- tion measurements with a wide q-range. J. Chem. Phys. 138, 074506 (2013)
7. Soper, A. K. The radial distribution functions of water as derived from radiation total scattering experiments: Is there anything we can say for sure? ISRN Phys. Chem. 2013 (2013)
8. Wiktor, J., Ambrosio, F. & Pasquarello, A. Note: As- sessment of the scan+ rvv10 functional for the structure of liquid water. J. Chem. Phys. 147, 216101 (2017)
9.Yao, Y. & Kanai, Y. Free energy profile of nacl in water: First-principles molecular dynamics with scan and wb97x-v exchange-correlation functionals. J. Chem. Theory Comput. 14, 884-893 (2018)
Acknowlegdements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Awards DE-SC0001137 and DE-SC0019394, as part of the CCS and CTC Programs. Sebastian Dick was supported by a fellowship from The Molecular Sciences Software Institute under NSF grant OAC-1547580.